
https://leetcode.com/problems/word-search/
Problem Statement:
Given an m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Examples
1:
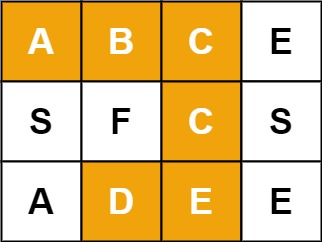
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true
Idea:
Here what we do is a breadth first search, but also marking our path as we going along. We keep progressing so long as the current spot in the grid is equal to the current letter in the target word. When we visit a cell, we mark it as visited and recursively search the neighbors. When we return from this, we set the cell back to the orignal value.
Solution:
class Solution {
public:
bool dfs(int row, int col, vector<vector<char>> &board, string & target, int index) {
if(index >= target.size()) {
return true;
}
if(row < 0 || col < 0 || row >= board.size() || col >= board.front().size() || board[row][col] != target[index]) {
return false;
}
board[row][col] = '$';
if(dfs(row - 1, col, board, target, index + 1) ||
dfs(row + 1, col, board, target, index + 1) ||
dfs(row, col + 1, board, target, index + 1) ||
dfs(row, col - 1, board, target, index + 1)
) {
return true;
}
board[row][col] = target[index];
return false;
}
bool exist(vector<vector<char>>& board, string word) {
for(int i = 0; i < board.size(); ++i) {
for(int j = 0; j < board.front().size(); ++j) {
if(dfs(i, j, board, word, 0)) {
return true;
}
}
}
return false;
}
};
Complexity Analysis:
Time
We look at every cell in the board, and looking at every cell is order O(M * N) where M and N are the dimensions of the grid.
And for each cell, we could potentially recurse L times where L is the length of the string.
Therefore the overall time complexity is (M * N * L)
Memory
O(L) stack space for recursive calls.



Comments
Nothing yet.