https://leetcode.com/problems/valid-parentheses/

Given a string s containing just the characters ‘(’, ‘)’, ‘{’, ‘}’, ‘[’ and ‘]’, determine if the input string is valid.

An input string is valid if:

Open brackets must be closed by the same type of brackets. Open brackets must be closed in the correct order. Every close bracket has a corresponding open bracket of the same type.

Idea:

If we see a closing parenthese, that means that the most recently seen opening parenthese must be it’s complement.

If not, we know the string does not have valid parantheses.

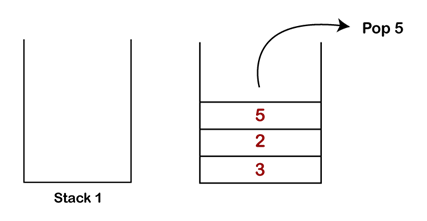
To do this, we use a stack and scan over the string. If the char is a opening paren, add it to the stack. If its a closing paren, see if the most recent open paren is it’s complement. If its not, return false. Otherwise pop the top of the stack.

At the end, we check the size of the stack. If its empty that means every opening paren found its complement and thus the string is valid.

Solution:

class Solution {
public:
    bool isValid(string s) {
        deque<char> deque;

        for(auto &current : s) {
            if (isOpenBracket(current)) {
                deque.push_back(current);
             } else {
                if (deque.empty() || !isComplement(current, deque)) {
                    return false;
                }
            }
        }

        return deque.empty();
    }

    bool isOpenBracket(const char & c) {
        return (c == '(' || c == '[' || c == '{');
    }

    bool isComplement(const char & closed, deque<char> & deque) {
        const char open = deque.back();
        deque.pop_back();

        if (open == '(' && closed != ')') {
            return false;
        } else if (open == '[' && closed != ']') {
            return false;
        } else if (open == '{' && closed != '}') {
            return false;
        }
        return true;
    }
};

Complexity Analysis:

Time

O(N) to loop over the string

Constant time to check if char is open paren or closed paren (and if closed that it has a complement)

O(N) + c = O(N)

Memory

O(N) in the worst case. Ex ("((((")