https://leetcode.com/problems/sum-root-to-leaf-numbers/
Problem Statement:
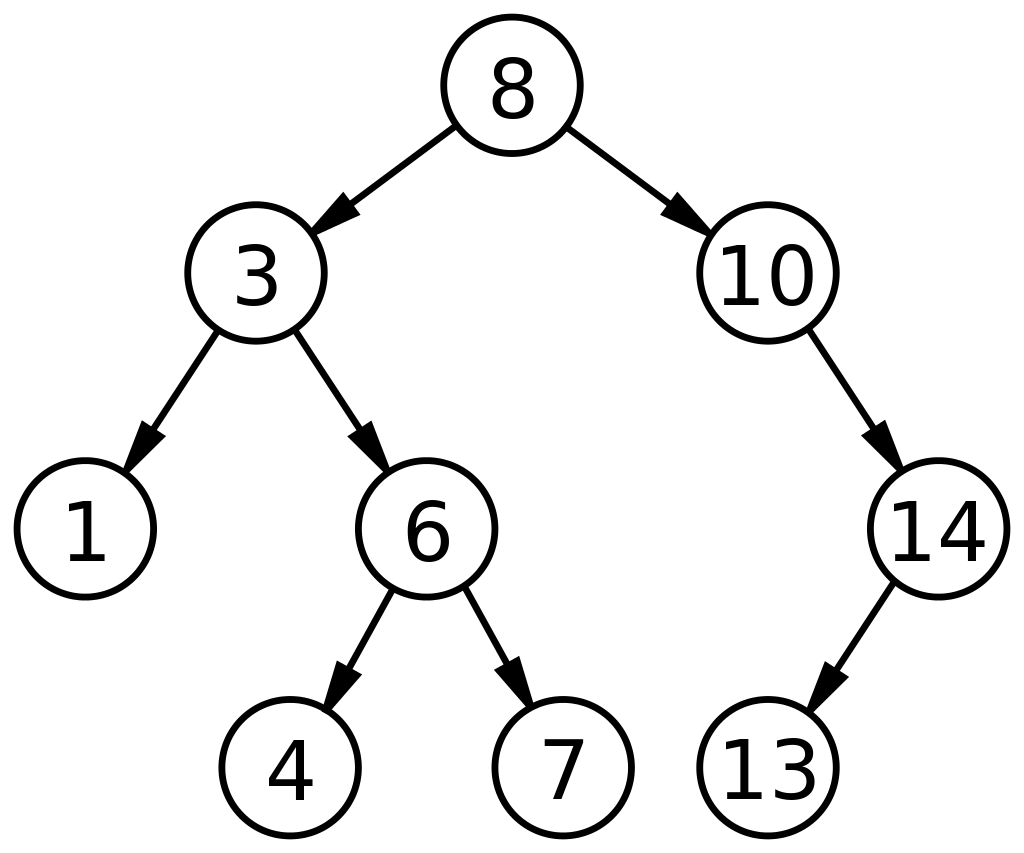
Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.
An example is the root-to-leaf path 1->2->3 which represents the number 123.
Find the total sum of all root-to-leaf numbers.
Note: A leaf is a node with no children.
Examples
1:
Input: [1,2,3]
1
/ \
2 3
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.
2:
Input: [4,9,0,5,1]
4
/ \
9 0
/ \
5 1
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.
Idea:
The idea is traverse our tree, using any tree traversal algorighm. I choose dfs, and also I directly change the values of our tree.
- If we reach non-existing node (None), we just return back.
- If we reached leaf, that is it do not have any children, return value of this node.
- Update values for left and right children if they exist.
- Finally, call function recursively for left and right children and return sum of results for left and right.
Solution:
class Solution {
public:
void findPath(TreeNode* root, string &path, int &total) {
if(root == nullptr) return;
path += std::to_string(root->val);
if(root->left == nullptr && root->right == nullptr) {
total += stoi(path);
}
findPath(root->left, path, total);
findPath(root->right, path, total);
path.pop_back();
}
int sumNumbers(TreeNode* root) {
string path;
int total = 0;
findPath(root, path, total);
return total;
}
};
TODO: Look at Morris Preorder Traversal.



Comments
Nothing yet.