https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/

Problem Statement:

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example:

Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]

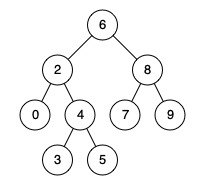
1:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Idea:

My approach was recursive in nature, but prunes the tree and can achieve O(log N) time and space complexity (call stack) if used on a balanced tree.

The idea is to check if p and q are in different subtrees. If p is on the left and q is on the right, or vice versa, this means that we have found the solution. The first node in which p and q are in different trees is by definition their least common ancestor.

Therefore, we use the sorted nature of the BST to go left or right if p and q are on the same side of the tree. If they aren’t on the same side, we’ve found the solution.

If we never find such a node, return nullptr;

As a side note, I chose to make p and q global to avoid passing them along the call stack in the recursive function.

Solution:

class Solution {
public:
    int PVAL, QVAL;
        
    TreeNode* findLCA(TreeNode* root) {

        if(!root) return nullptr;

        if((PVAL >= root->val && QVAL <= root->val) || (PVAL <= root->val && QVAL >= root->val)) {
            return root;
        }
        
        if(PVAL > root->val) {
            return findLCA(root->right);
        } else {
            return findLCA(root->left);
        }

    }
    
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        PVAL = p->val;
        QVAL = q->val;
        return findLCA(root);
    }
};

Complexity Analysis:

Time

Here worst case is O(N) if our tree is an unbalanced stick where p/q happen to be very far from the root.

With idea situations, search space is cut in half each time provided the tree is balanced so we see O(logN) time complexity.

Complexity is directly related to the ability so find the solution.

Memory

O(N) unbalanced stick with p & q far from root. O(logN) with balanced tree.